基于这本书：

关于CORDIC算法，这里有一个很好的中文PPT：

在本章，我们将会学习一种用于计算三角函数等许多特殊函数的优雅收敛方法，即CORDIC算法。其计算延迟与硬件成本开销只比除法或平方根算法略高一些。

考虑上图Fig 22.1中的向量 OE^{(i)} ，其一个端点为原点 O ，另一个端点为坐标为 (x^{(i)},y^{(i)}) 的 E^{(i)} 。将 OE^{(i)} 绕原点旋转 \alpha ^{(i)} 度后，我们的到了新的坐标为 (x^{(i+1)},y^{(i+1)}) 的端点 E^{(i+1)} ，其满足：

变量 z 用于标记旋转诺干步后与目标旋转角度间的差值，初值 z^{(0)} 即为我们设定的旋转目标角度， z^{(i)} 即为旋转 i 次后于目标角度所差的角度，我们希望 z^{(m)} 趋于0，即 (x^{(m)},y^{(m)}) 将会是 (x^{(0)},y^{(0)}) 旋转 z^{(0)} 度后的点。

CORDIC算法的名称来源于 1950 年代末设计的坐标旋转计算机（coordinate rotation digital computer）。如图Fig 22.1所示，旋转被“伪旋转（pseudorotation）”代替了，伪旋转也能将点旋转 \alpha^{(i)} 度（ E 伪旋转后为 E' ），但被旋转的向量长度将增加

伪旋转的计算更简单，如下：

至于伪旋转的推导，将真旋转中的 x^{(i+1)},y^{(i+1)} 分别乘以 (1+\tan^2\alpha^{(i)})^{1/2} ，就能得到它。

令 x^{(0)}=x,y^{(0)}=y,z^{(0)}=z ，则经 m 次真旋转后将有：

其中 \alpha^{(m)} 是每次旋转的度数。

对于伪旋转，我们有：

可以看出，真实旋转 m 次，与伪旋转 m 次后的坐标，仅相差了一个

我们把该 K 称为伸缩因子。

而且稍后我们可以看到，通过选取特定旋转角度 \alpha^{(i)} ，伪旋转的计算将只涉及移位与加法以及简单的查表，并且也能预先计算其对应的伸缩因子。

为简化伪旋转，我们取 \alpha^{(i)} 为满足 \tan \alpha^{(i)}=d_i2^{-i} 的角度，其中 d_i\in \{-1,1\} ，基于此伪旋转迭代方程将简化为：

于是 x^{(i+1)},y^{(i+1)} 的计算将分别只需用一个1bit移位与一个加减法。对于 z^{(i+1)} ，我们可以将 e^{(i)}=\tan^{-1}2^{(-i)} 预先计算并存储于查找表中，于是 z^{(i+1)} 将只需要一个加减法与一次查表。

下表展示了 e^{(i)} 从i=0到9的预计算近似值：

于是总的算下来，一次伪旋转只需要 3次加减法、2次1位移位、1次查表。

伸缩因子的预计算

现在我们来看伸缩因子

显然只要每次旋转的角度的绝对值（即 |\alpha^{(i)}| ）确定了，我们就可以预先计算 K。例如们可以将30°近似展开为以下角度之和：

旋转模式（rotation mode）

d_i 指示了每次伪旋转的方向，显然应该朝着目标点旋转，因此伪旋转迭代中的 d_i\in \{1,-1\} ，将由 z^{(i)} 的符号决定，即 d_i=sign(z^{(i)}) ，这容易让人想到不恢复余数除法。

上表就展示了使 z 趋向0的 d_i 的选择（正负号）。

在CORDIC术语中，前面使 z 收敛至 0的 d_i 选择规则被称之为“rotation mode（旋转模式）”。基于此我们将CORDIC迭代改下如下：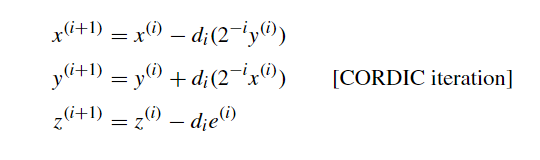

其中 e^{(i)}=\tan^{-1}2^{-i} 。

在旋转模式下进行 m 次迭代后 z^{(m)} 将逼近0，诺我们有 \sum_{}^{}{\alpha^{(i)}} ，则前面带[*]的CORDIC式将变为：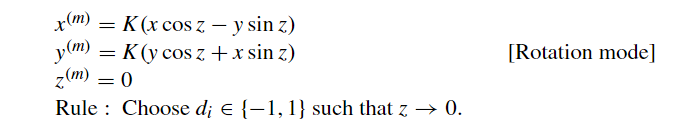

其中K位常量 K=1/646760258121\dots 。

通过特殊初值消去伸缩因子K

然后，我们可以令初值 x^{(0)}=1/K=0.607252935\dots 以及 y^{(0)}=0 以消去上式中的K。于是CORDIC算法只需要n次仅含移位和加减法以及查表的迭代，就能计算 cos z和sin z。然后我们可以再通过sin x/cos x 得到tan x。

精度与收敛的分析

诺三角函数结果需要精确到 k bits，则需要 k 轮CORDIC迭代。这是因为对于较大的 i ，我们有 \tan^{-1}2^{-i}\approx 2^{-i} ，所以对于 i>k ，其有关导致的 z 的变化将小于 ulp。

在旋转模式下，z也可能收敛至0，因为Table 22.1中每个角度都大于前一个角度的一般，或者说每个角度都小于后面所有角度之和。对于此，收敛域为 -99.7^\circ\le z\le 99.7^\circ ，这个范围包括了-90°到+90°（或者弧度制地[-π/2,π/2]），因此我们可以利用三角函数诱导公式将任意角度压缩至该范围内：

值得注意的是，诺角度是以派弧度的倍数来表示的，那么这些变换就会非常简单。例如z=0.2实际上意味着z=0.2π，默认角度都乘了一个π。于是收敛域变成了[-1/2,1/2]此范围外的数仅需加减代表弧度π倍数的整数就可以将其调整在范围内。我们会在Section 23.1中讨论有关函数求值范围约化（range reduction）更一般的方法。

向量模式（vectoring mode）

向量模式是CORDIC迭代的第二种方法。此时我们通过取 d_i=-sign(x^{(i)}y^{(i)}) 以使y向0收敛。经m次向量模式迭代后，我们有 \tan(\sum_{}^{}{\alpha^{(i)}})=-y/x ，即意味着：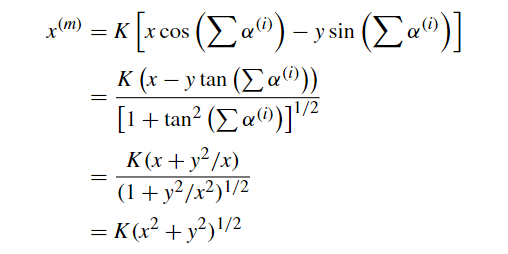

于是前文中带[*]的CORDIC等式将变为：

在向量模式下，我们可以令 x^{(0)}=1,z^{(0)}=0 ，然后进行迭代，以计算 \tan^{-1}y 。这个计算总是收敛的，但我们也可以利用等式：

以限制所遇的定点数的范围。除此之外我们也将在后面的Section 22.5看到，CORDIC也可用于计算其它反三角函数。

三维CORDIC

前面讨论的都是2维空间（即平面）上的旋转与伪旋转。但许多计算机需要考虑三维空间中的旋转或者其它几何操作。关于这些类似的三维方法及其应用的讨论可以参考[Lang05]。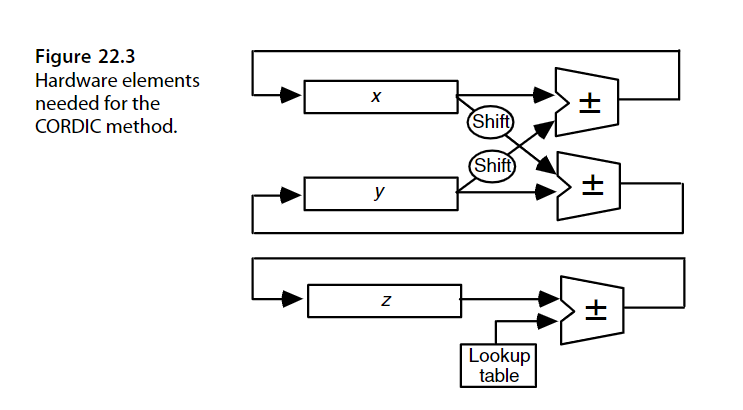

上图展示了一个CORDIC算法的简单硬件实现。如果速度降低三倍是可接受的，也可以仅用一个加法器分别处理x,y,z的迭代。在极端情况下，我们可以直接用普通CPU中的算术逻辑核心与通用寄存器组在固件（微程序）甚至软件中实现CORDIC迭代。上图中的加法器也是可以位串行的，于是kbits操作数将导致需要O(k^2)拍时钟完成k次迭代，这对手持式计算器等应用情景来说是可接受的，因为即使是几万个时钟周期也只会是一秒的一小部分，人类用户难以察觉。

Section 22.2所介绍的基本CORDIC方法可以被推广为一个更强大的函数求值工具，广义CORDIC的定义如下：

相较于基础CORDIC迭代，我们在广义CORDIC迭代中重新定义了 e^{(i)} ，并引入了参数 μ：

用于指定CORDIC形式，下图Fig 22.4展示了广义CORDIC形式的不同转动方式：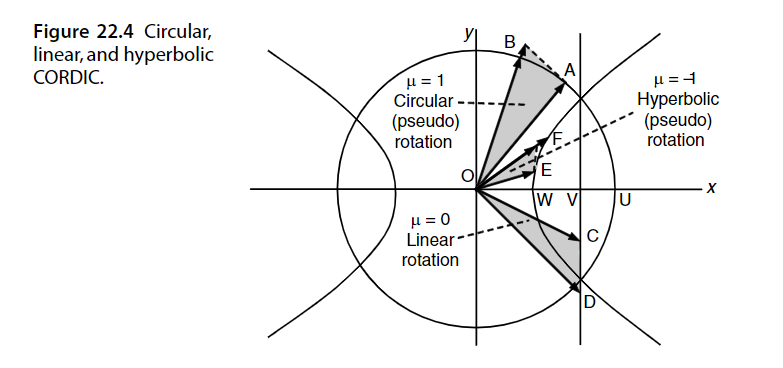

圆CORDIC

对于 μ=1 时的圆情况，我们引入了伪旋转，而导致每步迭代会使向量长度扩张一个因子 (1+\tan^2\alpha^{(i)})^{(1/2)}=1/\cos \alpha^{(i)} ，最终会导致伪旋转结果与正确结果偏离一个伸缩因子系数 K=1.646760258121\dots 。此时向量长度即为我们所熟知的 R^{(i)}=\sqrt{(x^{(i)})^2+(y^{(i)})^2} 。如图Fig 22.4，旋转角度∠AOB可基于扇形AOB的面积定义为：

为方便比较，再次列出以下方程，他们代表了CORDIC旋转的结果：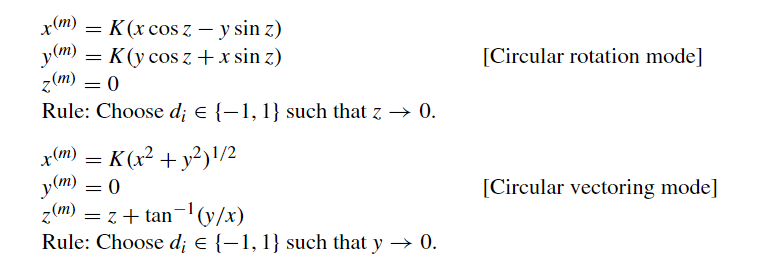

线性CORDIC

在 μ=0 对应的线旋转中，向量的端点将保持在直线 x=x^{(0)} 上，且向量“长度”将定义为 R^{(i)}=x^{(i)} 。因此，向量长度将总为OV的真是长度，并且伸缩因子为1（在这种情况下，我们的伪旋转就是真实的线性旋转）。

下方程组展示了线性CORDIC的旋转迭代过程：

因此，线性CORDIC可用于计算：乘法（旋转模式，y=0）、乘加（旋转模式）、除法（向量模式，z=0）、除加（向量模式）。

双曲CORDIC

在 μ=-1对应的双曲旋转中，旋转“角度”∠EOF可基于双曲扇形EOF的面积定义为：

而向量长度将定义为 R^{(i)}=\sqrt{(x^{(i)})^2-(y^{(i)})^2} ，而伪旋转在每次迭代中引入的偏差系数为 (1-\tanh^2\alpha^{(i)})^{1/2}=1/\cosh\alpha^{(i)} 。由于 \cos h\alpha^{(i)}>1 。向量长度实际上发生了收缩，而最终的总伸缩因子为 K'=0.8281593609602\dots 。

下方程组展示了双曲CORDIC的旋转迭代过程：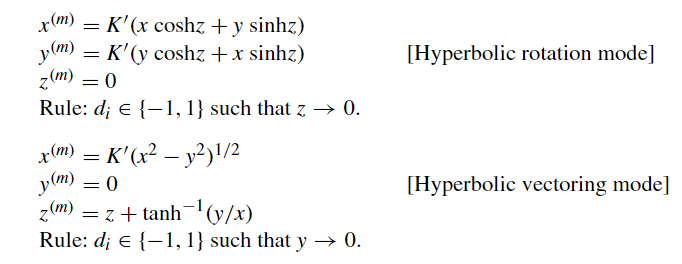

因此双曲CORDIC可用于计算：sine和cosine（旋转模式，x=1/K'，y=0）、 \tan ^{-1} （向量模式，x=1，z=1）。也可以基于此间接计算其它函数。

收敛性分析

Section 22.2讨论了圆CORDIC迭代的收敛性。对于适当限制的 z（旋转模式）或 y（向量模式），线性CORDIC迭代通常是收敛的。

对于双曲CORDIC，确保收敛有点棘手，因为 \tan^{-1}(2^{-(i+1)})\ge 0.5\tan^{-1}(2^{-i}) ，而对应的tanh形式，即 \tanh^{-1}(2^{-(i+1)})\ge0.5\tanh^{-1}(2^{-i}) 通常不成立。

一个相对简单的方法是重复 i=4,13,40,121,...,j,3j+1,... 步骤以确保收敛（每一项是上一项的三倍加一），即，对于上述 i 值的迭代周期，我们将其执行两次。这些重复对性能的性能的影响不大，因为在实践中我们通常总是 m

于是，通过在每次迭代中使用额外的移位/加法来更新伸缩因子的平方，我们不再只能使用一次旋转角度（或在双曲伪旋转中某些迭代恰好使用两次）。最后，迭代之后，我们可能要将结果除以由此得到的 (K^{(m)})^2 的平方根。考虑到维护这些额外变量所需的调整和计算，包括开平方和除法，这些修改通常是不值得的，常量伸缩因子几乎总是优于变量伸缩因子的。

减少迭代次数

也存在一些用于减少常熟因子CORDIC迭代次数（k次）的加速方法。圆CORDIC（在旋转模式下）的一个想法就是，首先像往常一样进行 k/2 次迭代，但将剩下的 k/2 步迭代合并为一个步骤（需要乘法）：

这是可行的，因为对于非常小的 z，我们有 \tan^{-1}z\approx z\approx \tan z 。伸缩因子 K 也没问题因为 e^{(i)}

其中 u^{(m)} 趋于0时我们有 v^{(m)}=ve^u ，而实现指数函数的计算（我们会在Section 23.3证明这点）。

由于 \cos z+j\sin z=e^{jz} ，其中 j=\sqrt {-1} 。我们可以同时计算 \cos z,\sin z ，通过在上迭代中设置初值 v^{(0)}=1,u^{(0)}=jz ，并使用复数计算。

现在考虑等式：

其中 \theta=\tan^{-1}(b/a) ，并假设我们取：

其中 d_i\in\{-1,1\} 。

定义 g^{(i)}=\tan^{-1}(d_i2^{-i}) ，则负数 c^{(i)} 可写为下形式：

于是我们有：

为简化计算 v^{(i+1)} 所需的乘法，我们可以将第二个迭代式替换为：

在其右侧乘以 \sqrt{1+2^{-2i}} ，会将 v^{(m)}=v^{(0)}e^{jz} 变为：

因此，通过将替代 v^{(0)}=1 为 v^{(0)}=1/(\prod_{i=1}^{m-1}\sqrt{1+2^{-2i}}) ，我们仍然可以得到 v^{(m)}=e^{jz}。注意其中的 \prod_{i=1}^{m-1}\sqrt{1+2^{-2i}} 在CORDIC术语中，就是所谓的伸缩因子 K，并且其中的复数乘法

可以按实部和虚部拆开，而得到：

还要注意的是，由于变量 u 被初始化为虚数 jz ，且只有 jg^{(i)} 会从中减去，以使其收敛至0。我们可以忽略因子 j，并直在实变量 z^{(i)}=-ju^{(i)} 上执行实数计算，而不是初始化 z^{(0)}=z 。这就完成了圆CORDIC的代数推导。

[Andr98] Andraka, R., “A Survey of CORDIC Algorithms for FPGA Based Computers,”Proc.6th Int’l Symp. Field Programmable Gate Arrays, pp. 191–200, 1998.

[Ante97] Antelo, E., L. Villalba, J. D. Bruguera, and E. L. Zapata, “High Performance RotationArchitectures Based on the Radix-4 CORDIC Algorithm,”IEEE Trans. Computers,Vol. 46, No. 8, pp. 855–870, 1997.

[Ante00] Antelo, E., T. Lang, and J. D. Bruguera, “Very-High Radix Circular CORDIC:Vectoring and Unified Rotation/Vectoring,”IEEE Trans. Computers, Vol. 49, No. 7,pp. 727–739, 2000.

[Dawi99] Dawid, H., and H. Meyr, “CORDIC Algorithms and Architectures,” inDigital SignalProcessing for Multimedia Systems, ed. by K. K. Parhi and T. Nishitani, pp. 623–655,Marcel Dekker, 1999.

[Dupr93] Duprat, J., and J.-M. Muller, “The CORDIC Algorithm: New Results for Fast VLSIImplementation,”IEEE Trans. Computers, Vol. 42, No. 2, pp. 168–178, 1993.

[Lang05] Lang, T., and E. Antelo, “High-Throughput CORDIC-Based Geometry Operations for3D Computer Graphics,”IEEE Trans. Computers, Vol. 54, No. 3, pp. 347–361, 2005.

[Lee92]Lee, J.-A., and T. Lang, “Constant-Factor Redundant CORDIC for Angle Calculationand Rotation,”IEEE Trans. Computers, Vol. 41, No. 8, pp. 1016–1025, 1992.

[Maze93] Mazenc, C., X. Merrheim, and J.-M. Muller, “Computing Functions cos−1and sin−1Using CORDIC,”IEEE Trans. Computers, Vol. 42, No. 1, pp. 118–122, 1993.

[Mull06] Muller, J.-M.,Elementary Functions: Algorithms and Implementation, 2nd ed.,Chapter 7, Birkhauser, 2006.

[Omon94] Omondi, A. R.,Computer Arithmetic Systems: Algorithms, Architecture andImplementations, Prentice Hall, 1994.

[Phat98] Phatak, D. S., “Double Step Branching CORDIC: A New Algorithm for Fast Sine andCosine Generation,”IEEE Trans. Computers, Vol. 47, pp. 587–603, 1998.

[Taka91] Takagi, N., T. Asada, and S. Yajima, “Redundant CORDIC Methods with a ConstantScale Factor for Sine and Cosine Computations,”IEEE Trans. Computers, Vol. 40,No. 9, pp. 989–995, 1991.

[Vach87] Vachss, R., “The CORDIC Magnification Function,”IEEE Micro, Vol. 7, No. 5,pp. 83–84, 1987.

[Vill98]Villalba, J., E. L. Zapata, E. Antelo, and J. D. Bruguera, “Radix-4 Vectoring CORDICAlgorithm and Architectures,”J. VLSI Signal Processing, Vol. 19, No. 2,pp. 127–147, 1998.

[Vold59] Volder, J. E., “The CORDIC Trigonometric Computing Technique,”IRE Trans.Electronic Computers, Vol. 8, No. 3, pp. 330–334, 1959.

[Vold00] Volder, J. E., “The Birth of Cordic,”J. VLSI Signal Processing, Vol. 25, No. 2,pp. 101–105, 2000.

[Walt71] Walther, J. S., “A Unified Algorithm for Elementary Functions,”Proc. AFIPS SpringJoint Computer Conf., pp. 379–385, 1971.

[Walt00] Walther, J. S., “The Story of Unified Cordic,”J. VLSI Signal Processing, Vol. 25,No. 2, pp. 107–112, 2000.